Quick Union: Exercise
- Explain the runtime improvements gained by using the heuristics for union-find operations.
- Define the iterated logarithm (log-star) function.
- Identify the amortized runtime of union-find operations.
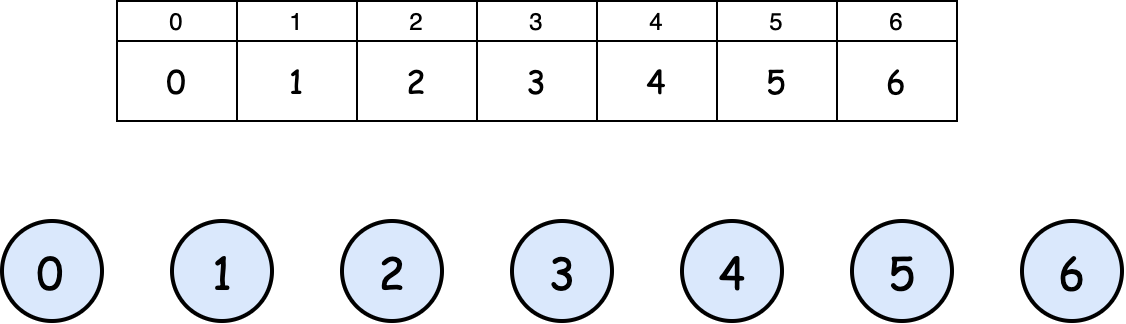
Suppose you have singleton sets with the values $0$ through $6$. Then, we apply the following operations.
union(0,5)
union(1,4)
union(2,3)
union(3,6)
union(4,6)
union(0,4)
Exercise Using both tree and array forms, show the result of each of the operations listed above, applying union-by-size and path compression heuristics.
Solution
Here is the start:
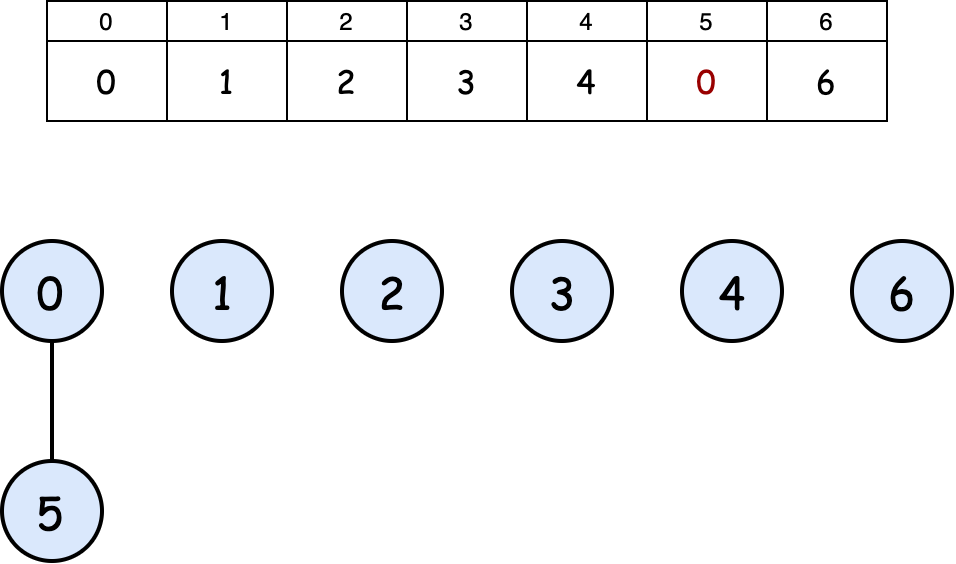
After union(0,5):
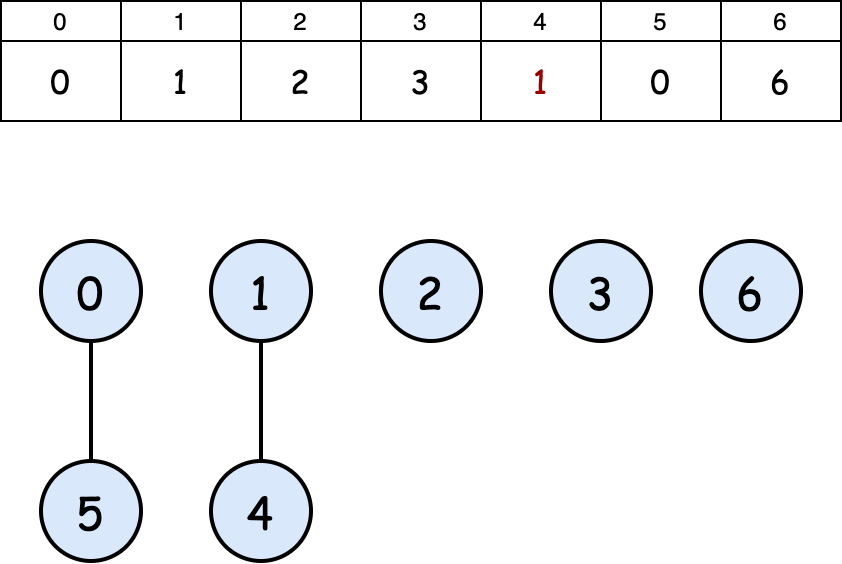
After union(1,4):
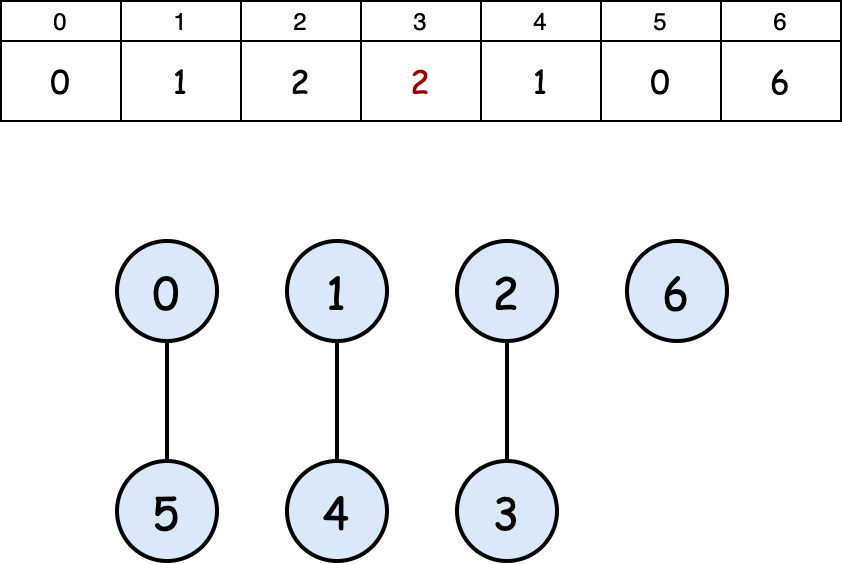
After union(2,3):
After union(3,6): notice the size of the component containing $6$ is smaller than the size of the component containing $3$. Therefore, the component containing $6$ is added to the root of the component containing $3$.
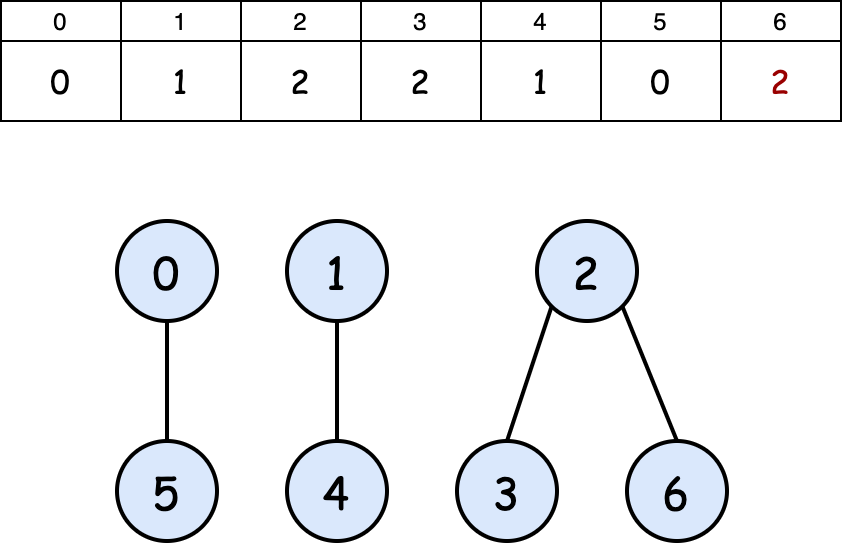
After union(4,6): notice the size of the component containing $4$ is smaller than the size of the component containing $6$. Therefore, the component containing $4$ is added to the root of the component containing $6$.
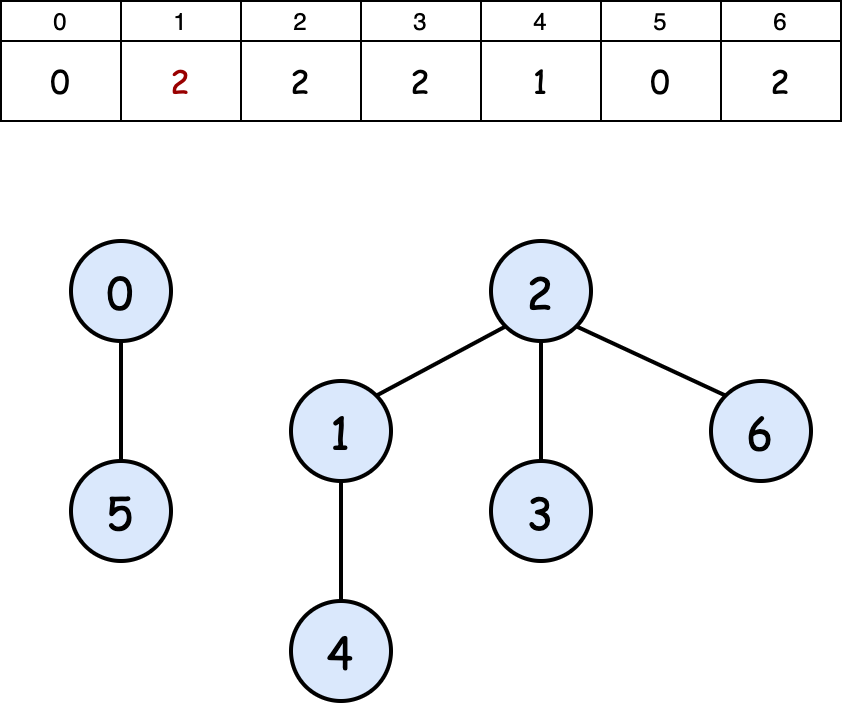
After union(0,4): notice as we find the root of the component containing $4$, we apply path compression.
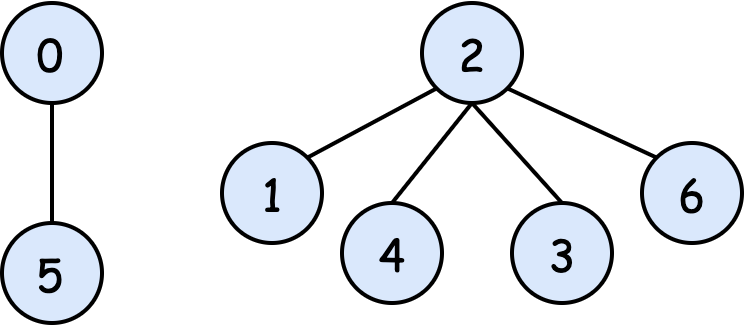
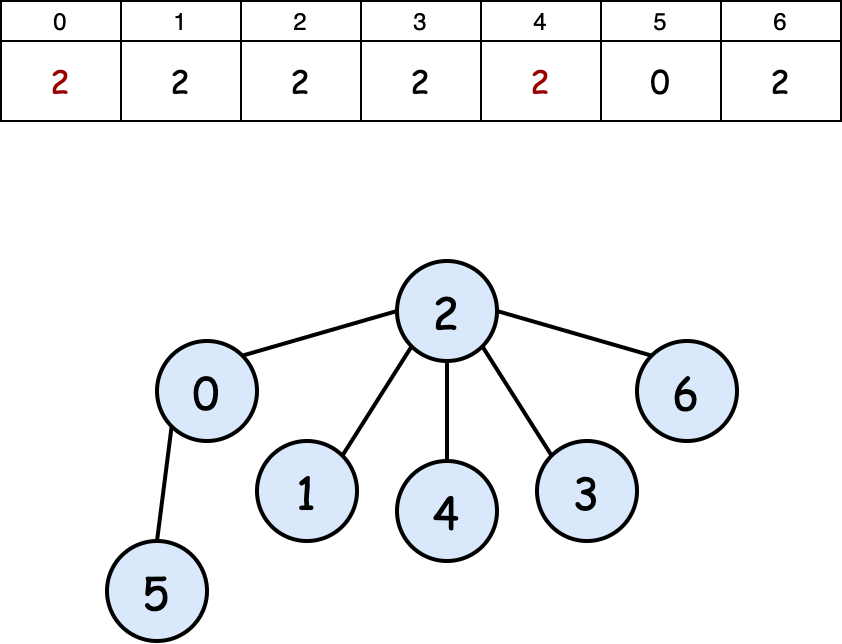
Then, as the size of the component containing $0$ is smaller than the size of the component containing $4$, the component containing $0$ is added to the root of the component containing $4$.
Note: Another common strategy to start the union-find data structure is to have the root of each component to have an ID of $-1$. This way, we can easily identify the root of a component.