Heapify: A Linear-Time Operation
- Show Floyd's heapify is a linear-time operation.
Each node, in Floyd's algorithm, in the worst case, sinks to become a leaf. The sink operation involves repeatedly (recursively) swapping the value with one of the children. Let's make the following observation:
Each node at height $h$ makes at most $h$ swaps (down).
So if you are a leaf, at height $h=0$, you make no swaps down. If you are one level higher, at height $h=1$, you make at most one swaps down. And so on. Let's make the following observation:
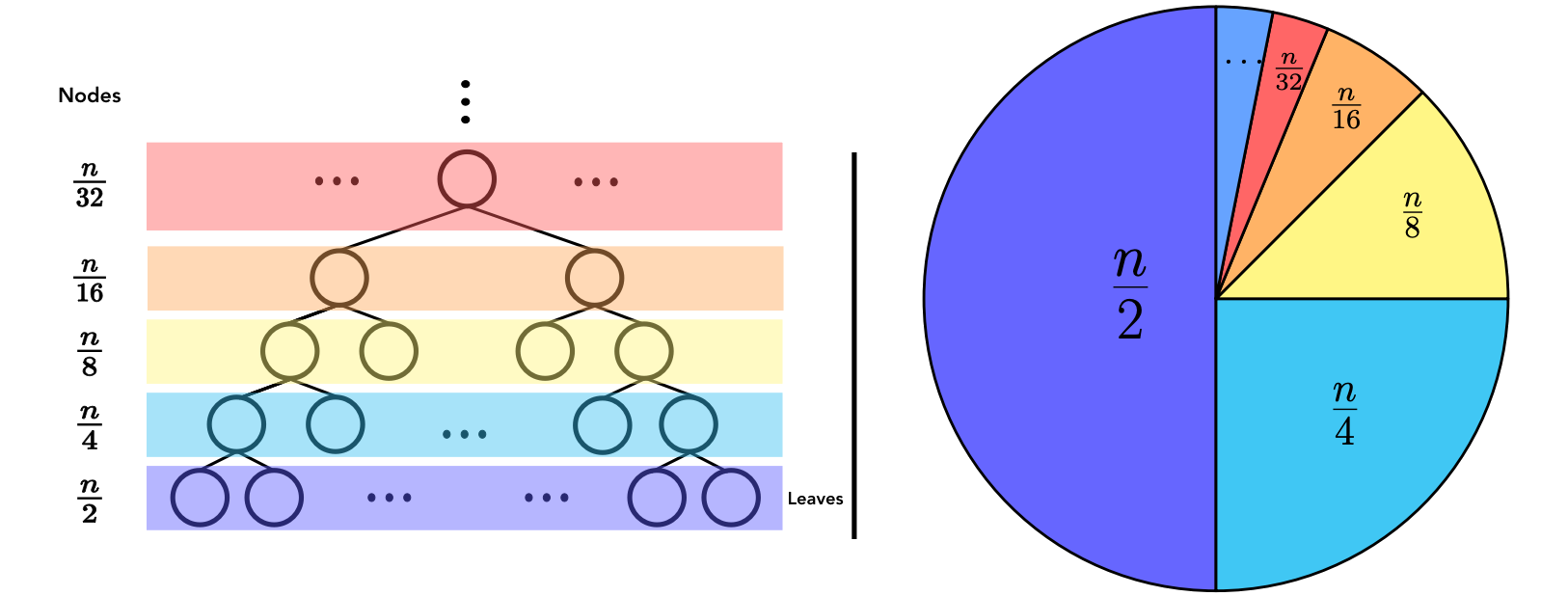
In a complete binary tree with $n$ nodes, there are $\left \lceil \frac{n}{2} \right \rceil$ nodes at height $h=0$ (leaves), $\left \lceil \frac{n}{4} \right \rceil$ nodes at height $h=1$, $\left \lceil \frac{n}{8} \right \rceil$ nodes at height $h=2$, $\dots$
In general, there are at most $\left \lceil \frac{n}{2^{h+1}} \right \rceil$ nodes of height $h$, so the cost of building a heap is
$$ \sum_{h=0}^{\left \lfloor \lg n \right \rfloor} \left \lceil \frac{n}{2^{h+1}} \right \rceil \Omicron(h) $$
We can rewrite the above expression as
$$ O \left ( \sum_{h=0}^{\left \lfloor \lg n \right \rfloor} \left \lceil \frac{n}{2^{h+1}} \right \rceil h \right ) $$
Since $n$ does not depend on the value of $h$, it can be moved out of the fraction
$$ O \left ( n \sum_{h=0}^{\left \lfloor \lg n \right \rfloor} \left \lceil \frac{h}{2^{h+1}} \right \rceil \right ) $$
Further observe that $\left \lceil \frac{h}{2^{h}\times 2} \right \rceil < \frac{h}{2^{h}}$ and we can use the upper-bound within big-O notation.
$$ O \left ( n \sum_{h=0}^{\left \lfloor \lg n \right \rfloor} \frac{h}{2^{h}} \right ) $$
Moreover,
$$ \sum_{h=0}^{\left \lfloor \lg n \right \rfloor} \frac{h}{2^{h}} < \sum_{h=0}^{\infty} \frac{h}{2^{h}} $$
And, we can use the upper-bound within big-O notation: $$ O \left ( n \sum_{h=0}^{\infty} \frac{h}{2^{h}} \right ) $$ It turns out the summation converges to $2$: (It is beyond the scope of this course to prove this, but you can check it out on Wolfram Alpha.)
$$ \sum_{h=0}^{\infty} \frac{h}{2^{h}} = 2 $$
Therefore, we get the following which means the heapify operation is linear time.
$$ O \left ( n \times 2 \right ) = O \left ( n \right ) $$
A more intuitive analysis
Let's consider a perfect binary tree; here is a less accurate but more intuitive analysis:
| Height | #nodes | worst-case #swaps | Total work |
|---|---|---|---|
| $0$ | $n/2$ | $n/2 \times 0 = 0$ | $0$ |
| $1$ | $n/4$ | $n/4 \times 1 = n/4$ | $n/4$ |
| $2$ | $n/8$ | $n/8 \times 2 = n/4$ | $n/2$ |
| $3$ | $n/16$ | $n/16 \times 3$ is close to $n/8$ | $n/2 + n/8$ |
| $4$ | $n/32$ | $n/32 \times 4 = n/8$ | $n/2 + n/4$ |
| $5$ | $n/64$ | $n/64 \times 5$ is close to $n/16$ | $n/2 + n/4 + n/16$ |
| $6$ | $n/128$ | $n/128 \times 6$ is close to $n/16$ | $n/2 + n/4 + n/8$ |
| $\vdots$ | $\dots$ | $\dots$ | $n/2 + n/4 + n/8 + \dots$ |
The summation for total work is in $\Omicron(n)$.
Resources
For a more detailed analysis of Floyd's algorithm, refer to Page 157 (Chapter 6, Section 3) of CLRS.