Homework 6: Graphs and Shortest Paths
In this assignment, you'll be implementing and working with graphs to solve real-world pathfinding problems.
Objectives
- Implement a Graph ADT using an incidence list representation for sparse graphs
- Design and write comprehensive unit tests for graph operations using test-driven development
- Implement Dijkstra's algorithm for finding shortest paths in weighted graphs
- Apply graph algorithms to solve real-world pathfinding problems using Baltimore street data
- Profile and analyze the performance of graph implementations and pathfinding algorithms
Important Dates
| Event | Day | Date | Time |
|---|---|---|---|
| Release | Wed | Apr 09 | 09:00 AM ET |
| Due | Fri | Apr 18 | 05:00 PM ET |
Homework Description
In this assignment, you will develop a robust graph implementation and use it to create a street navigation system. The project is structured in three main parts: First, you'll write comprehensive tests for a graph ADT. Then, you'll implement the graph ADT using an incidence list representation optimized for sparse graphs. Finally, you'll implement Dijkstra's shortest path algorithm and apply it to find optimal routes through Baltimore's street network. Throughout the assignment, you'll analyze the performance implications of your implementation choices and work with real geographic data.
You may use Java Collections (built-in data structures) in this homework (unless it is specified otherwise in any of the tasks).
Starter Code
Download the starter code from the following link: hw6.zip.
The starter code is a zip file named hw6-starter.zip. You must unzip this file. After unzipping, you will get a folder called hw6-starter. Open this folder as an IntelliJ project.
Tasks
This assignment consists of three main tasks:
- Test-First Development: Write a comprehensive suite of unit tests for the Graph ADT
- Implementation: Create an efficient sparse graph implementation using incidence lists
- Application: Implement Dijkstra's algorithm and apply it to street navigation
Each task builds upon the previous ones to create a complete street navigation system. Let's explore each task in detail.
Test-First Development: GraphTest
Your first task is to write a full suite of JUnit tests in the GraphTest.java file. A few examples are given; you must add many more tests there.
Be sure to test all operations of Graph ADT and test all exceptions for error situations.
Implementation: SparseGraph
Your second task is to complete the implementation of SparseGraph. You must follow the basic design for the incidence list representation outlined in the lecture notes. (Moreover, see the next section for a tip.)
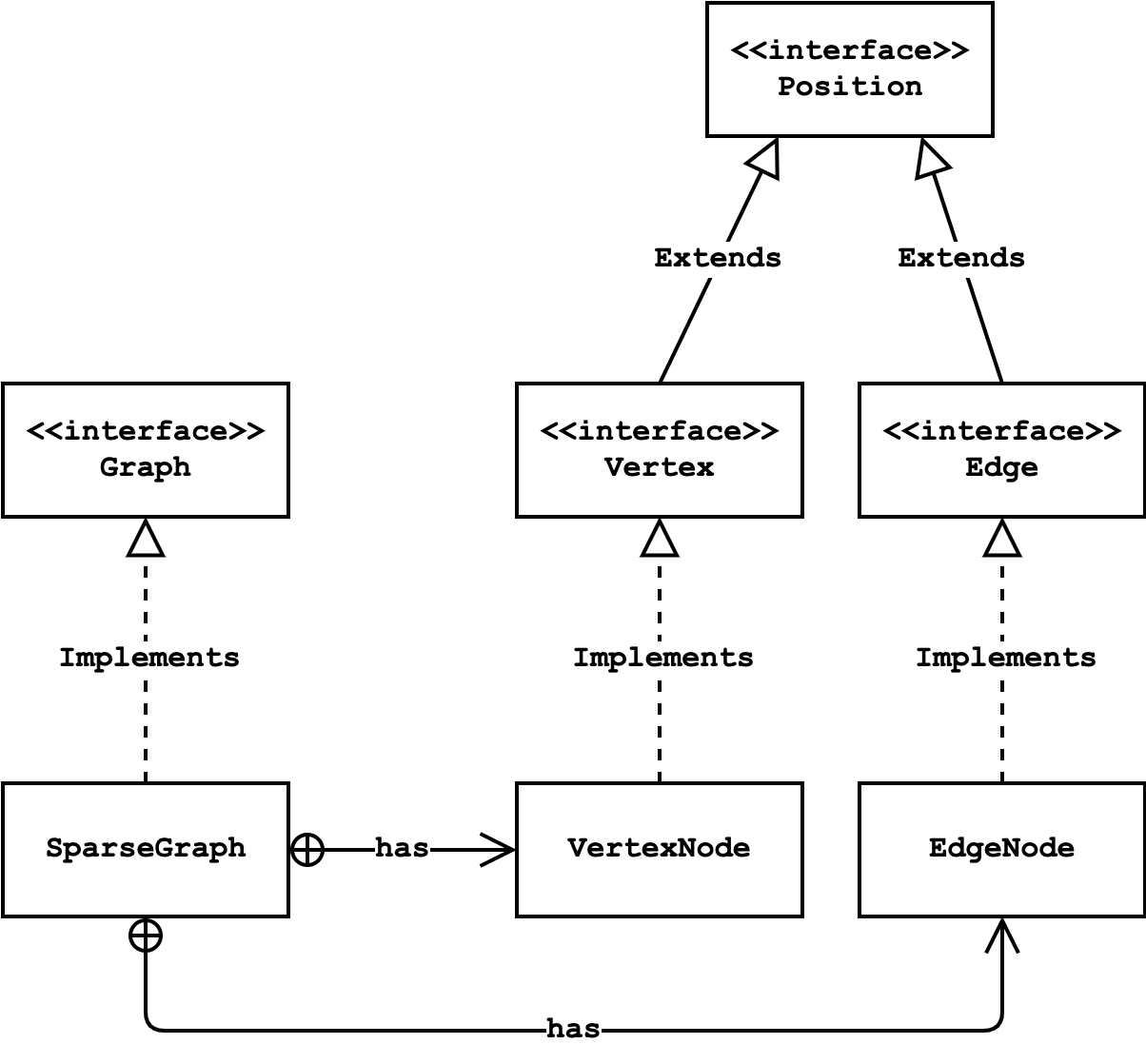
The SparseGraph class has two inner classes, VertexNode and EdgeNode, as well as private overloaded convert methods that convert a Position to these inner classes.
The following diagram represents the relationship between these classes:
The underlying idea is similar to, e.g., using the nested Node class for implementing the List interface:
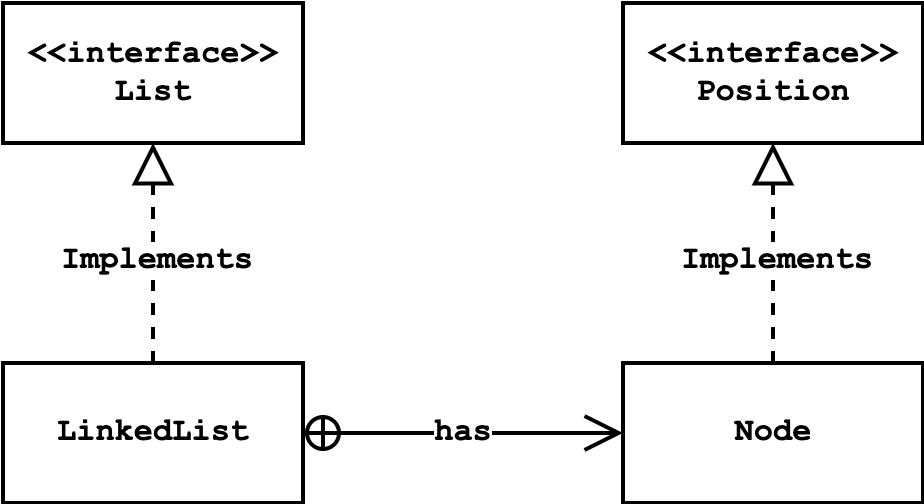
Note: The
Nodewas a nested class insideLinkedList, whereas we declaredVertexNodeandEdgeNodeas inner classes. Some things are easier with nested classes, and others are easier with inner classes. Here, our skeleton code uses inner classes. However, we could rewrite the provided code with nested classes.
Here is a tip for implementing SparseGraph: Maintain a collection of "vertices" and a collection of "edges." You can also maintain collections of "incoming" or "outgoing" (or both) edges associated with each vertex. As a special exemption from the usual rule regarding using built-in data structures, you are allowed to (and encouraged to) use Java's built-in data structures to build these internal "collections" of vertices/edges/etc.
The collections can be as simple as, e.g., an array of "vertices" or using more complex data structures (sets, maps, trees, hash tables, $\dots$). Just keep in mind: You aim for an "efficient" implementation of the Graph interface. We put "efficient" in quotes above because while ideally, all core graph operations take $\Omicron(1)$ time, the reality is that at least some operations will take more. For example, when inserting an edge, you need to check for duplicate edges, which may take $\Omicron(d)$ where $d$ is the indegree/outdegree of the vertices in question. Similarly, when removing an edge, you need to find the edge you're deleting in the incoming/outgoing edge lists of the vertices in question, again something that might take $\Omicron(d)$ time. Note that it is okay for clearLabel to be a linear-time operation.
Please refrain from asking whether your choice of internal data structures is correct/optimal in class, during office hours, or through the discussion forum. We want you to figure this on your own without the help of the teaching staff.
Graph ADT Iterator
The Graph ADT itself is not "iterable." Still, a number of its operations return Iterable to allow clients to explore certain aspects of a graph.
Suppose you use Java's built-in data structures to store collections of vertices/edges/etc. In that case, you can return the built-in iterator for those collections (yes, you are allowed to do so in this homework).
The problem with this approach is that Java provides a remove() method on its Iterators. A deviant client may use the "remove" method to "ruin" your internal representation of a graph. If you are using an Iterable for which the Iterator supports "remove," you will need to return an unmodifiable view of the specified Iterable collection.
You must search online to figure out how to do this. Hint: search for "java unmodifiable collections".
Please refrain from asking whether your finding is correct in class, during office hours, or through the discussion forum. We want you to figure this out independently without the help of the teaching staff.
GraphPrinter for Debugging
Your SparseGraph must pass all the tests you have written in GraphTest.java. You are welcome to add more tests to SparseGraphTest.java if you want to test something specific to the implementation, but you are not required.
You are encouraged to use IntelliJ debugger with visualization plugins such as jGRASP for debugging purposes. Additionally, we provided a GraphPrinter, which your SparseGraph's toString method relies on. The "printer" generates an output that can be used to "create" visualization of your graph using the GraphViz tool.
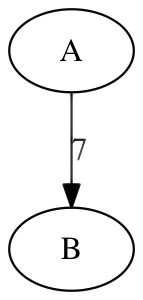
For example, for a simple Graph<String, Integer> into which the vertices $A$ and $B$, as well as an edge $7$ from $A$ to $B$, have been inserted, the string returned by toString() will have the following format:
digraph {
"A"
"B"
"A" -> "B" [label="7"];
}
You can copy the output above into, e.g., the online editor https://edotor.net/ (just one of many tools that support GraphViz rendering) to generate the following visualization.
Note that you are not required to do anything with GraphPrinter in this homework. In particular, do not write tests based on the output of toString methods. The "printing" is only provided as a tool to assist you in debugging, in case you need to visualize your graph.
Street Searcher
At this point, you have implemented the Graph interface using the incidence list representation. This representation is memory-efficient for sparse graphs, something we'll need for our application:
You will be touring the streets of Baltimore to find the shortest route from the JHU campus to other destinations around Baltimore.
This will require you to implement Dijkstra's algorithm for weighted shortest paths.
To do this, we have provided you a street map of Baltimore around the JHU campus. The original data was provided by the City of Baltimore, although we have focused it on a smaller region to make it more manageable. We have also simplified the formatting to make it easier to parse, although the GPS coordinates and street names are real.
The street map data is available in the file baltimore.streets.txt. Here are the first few lines of the file:
-76.6254,39.3373 -76.6255,39.3373 21.5510 39256:W_UNIVERSITY_PKWY
-76.6443,39.3096 -76.6443,39.3099 133.363 1530:1800_BLK_N_WOODYEAR_ST
-76.6177,39.3293 -76.6175,39.3292 70.8768 38350:E_34TH_ST
-76.6457,39.3149 -76.6454,39.3151 120.759 41431:AVALON_AVE
-76.6568,39.3244 -76.6569,39.3243 44.6691 37858:WAHOTAN_AVE
-76.6071,39.3115 -76.6061,39.3116 285.046 31155:800_BLK_E_NORTH_AVE
Each line in the file defines a road segment. The first pair of numbers represents the GPS coordinates (longitude and latitude) of the beginning of the road segment. The second pair of numbers is the end of the road segment. The following number is the length of the road segment in meters. The final field is the name of the road segment. All road segment names start with a unique integer index (the same index used on the City of Baltimore website). However, not every road segment has an English name.
Notice that this is an edge-oriented representation of the street network graph. Nodes in the graph are intersections, and the edges represent the road segments that connect the intersections.
Aside: Some road segments form dead-ends, especially alleys that don't connect to other roads.
Note that while we are using GPS coordinates to define the start and end of each road segment, you can treat them as strings!
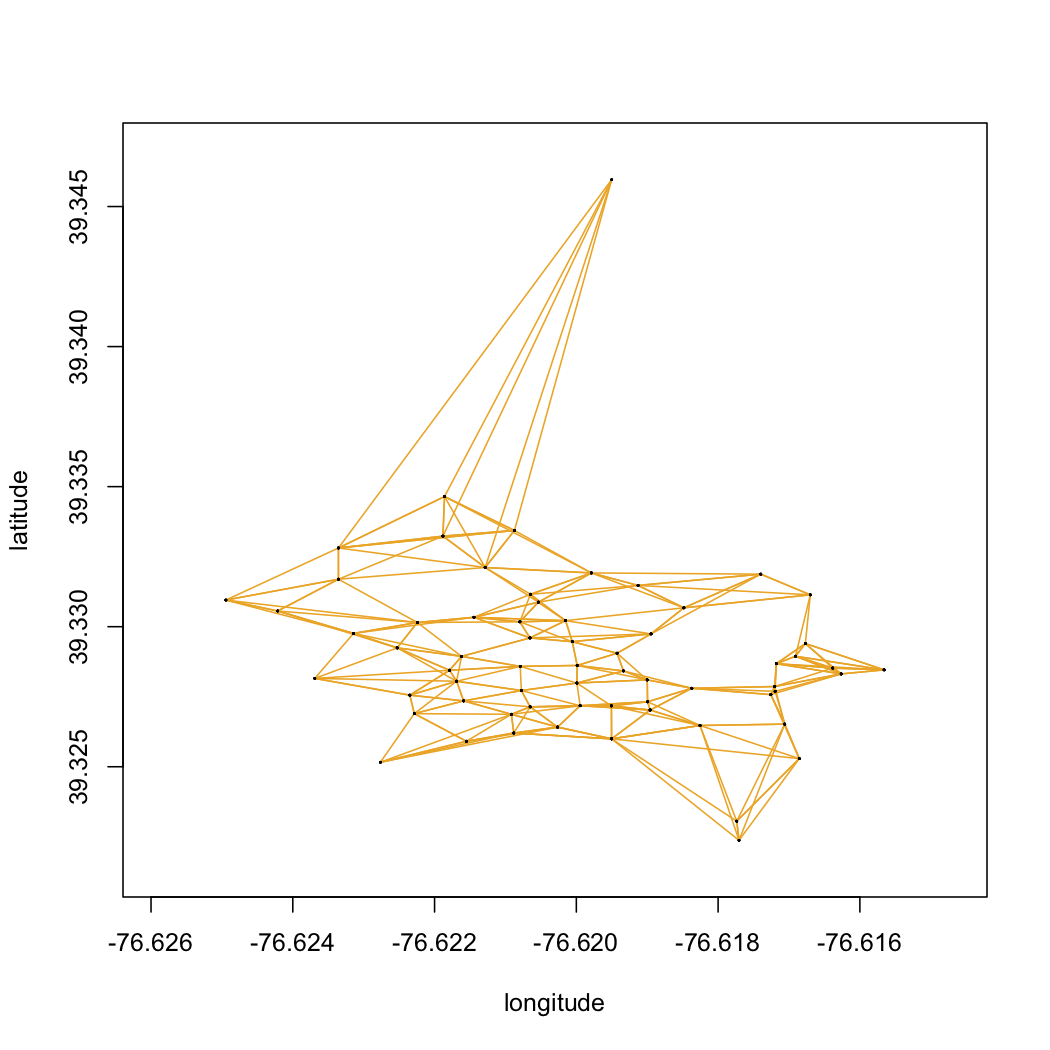
For reference, we have plotted the roadmap file here:
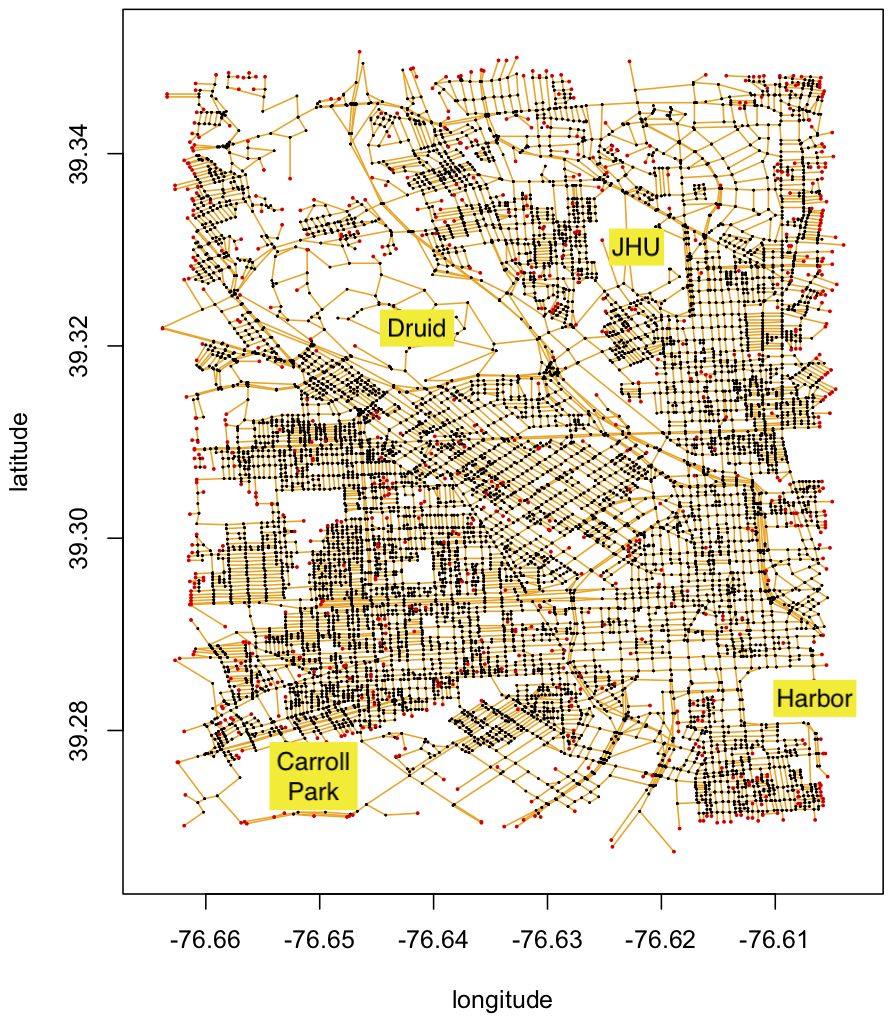
The orange lines represent the data in the baltimore.streets.txt file. The black dots highlight intersections where two or more road segments come together. The red dots highlight when a road segment does not intersect any other road segments. We have also highlighted a few landmarks (JHU, the Harbor, Druid Park, and Carroll Park) to orient you to the road map.
We have provided a smaller file representing the walking paths of the JHU campus called campus.paths.txt. It follows the same formatting as the larger street map but can be helpful for testing purposes.
Shortest Path
For this task, you'll be completing the findShortestPath method in the provided DijkstraStreetSearcher.java file. The method must implement Dijkstra's algorithm to find the shortest path between two locations within a street graph. To simplify the coding, you can assume that the graph search will start and end at intersections between different road segments and not at arbitrary GPS coordinates.
Note that DijkstraStreetSearcher extends StreetSearcher and implements its abstract method findShortestPath. Be sure to not change any of the methods in StreetSearcher since our test code will be calling these methods directly. Moreover, study the implementation of StreetSearcher, particularly the "Notes" comment block placed at the top of the class declaration.
The notes highlight how the vertex "label" is meant to store the edge into it on the path found and how the edge "label" is meant to store the road length. Look at the pseudocode for Dijkstra's algorithm (from lecture) and figure out what quantities will be stored in "labels" of vertices/edges. The labels will eliminate the need for a few of the auxiliary data structures for Dijkstra's algorithm. Regarding additional data structures, think of how you might use PriorityQueue to implement Dijkstra's algorithm. As with the implementation of SparseGraph, you are allowed to use Java's built-in data structures to implement Dijkstra's algorithm.
You can try the StreetSearcher program by running the Driver program in the experiment package.
Note: If any of the auto-tests fail, you can experiment with the Driver program (see the next section) in an attempt to debug your implementation. It may not be feasible to debug your application using the provided data files. Instead, you can create your data files to create a tiny graph with $4$ or $5$ road segments. Then, gradually work up to the larger ones as you become more sure things are working well. Then, perhaps try the entire dataset.
Experiment
Once your implementation of Dijkstra's algorithm is complete, run the Driver program. The output should print the total path distance followed by the names and lengths of the roads taken. For example, with the default values we provided in Config.java, the StreetSearcher will search the campus map and output the path from Malone Hall to the Undergraduate Teaching Labs:
Config: campus.paths.txt from -76.620883,39.326204 to -76.620647,39.331158
Network Loaded: 414 roads, 65 endpoints
Total Distance: 599.0428
58.16 Malone_Hall--Shriver_Hall
89.26 Shaffer_Hall--Shriver_Hall
90.09 Maryland_Hall--Shaffer_Hall
69.82 Maryland_Hall--Krieger_Hall
94.58 Remsen_Hall--Krieger_Hall
84.02 Remsen_Hall--Dunning_Hall
113.11 Undergraduate_Teaching_Labs--Dunning_Hall
You can control what data file and endpoints the Driver program uses through the Config.java file:
public static Config getConfig() {
/* Sample valid endpoints */
return new Config("campus.paths.txt", "-76.620883,39.326204", "-76.620647,39.331158");
}
There are several data files in src/main/resources:
baltimore.streets.txt
baseball.txt
broken.txt
campus.paths.txt
If the start and destination are the same, you get "No path found":
Config: campus.paths.txt from -76.620883,39.326204 to -76.620883,39.326204
Network Loaded: 414 roads, 65 endpoints
No path found
If the start or destination is invalid, your code should print the invalid endpoint:
Config: campus.paths.txt from -76.620883,39.326224 to -76.620883,39.326204
Network Loaded: 414 roads, 65 endpoints
Invalid Endpoint: -76.620883,39.326224
If there is no path between endpoints, your code should print "No path found":
Config: broken.txt from 1 to 4
Network Loaded: 8 roads, 5 endpoints
No path found
Profiling
The choices you make for implementing Graph ADT and Dijkstra's algorithm will affect the performance of your program. Look inside performance package (under test folder); we provide two crude profilers SystemRuntimeTest and MemoryMonitorTest. These profiles are not as sophisticated as JMH is. They are designed to provide a proxy measure to the performance of your program. Both SystemRuntimeTest and MemoryMonitorTest run your program with whatever configurations you provide in the Config.java file. Note that as before, you should rebuild your project after changing the Config.java file to ensure the results are accurate.
For example, on my computer, my implementation of the Graph ADT and the Dijkstra's algorithm, with the default configuration we provided in Config.java, produced the following outputs:
~~~ SystemRuntimeTest ~~~
Config: campus.paths.txt from -76.620883,39.326204 to -76.620647,39.331158
Loading network took 37 milliseconds.
Finding shortest path took 2 milliseconds.
~~~~~~ END ~~~~~~
~~~ MemoryMonitorTest ~~~
Config: campus.paths.txt from -76.620883,39.326204 to -76.620647,39.331158
Used memory: 12536.33 KB (Δ = 0.000)
Instantiating empty Graph data structure
Instantiating empty StreetSearcher object
Used memory: 12710.46 KB (Δ = 174.133)
Loading the network
Used memory: 13952.19 KB (Δ = 1241.727)
Finding the shortest path
Used memory: 14030.62 KB (Δ = 78.430)
Setting objects to null (so GC does its thing!)
Used memory: 13912.55 KB (Δ = -118.063)
~~~~~~ END ~~~~~~
Each time you run these profilers, you will get slightly different measurements. And, occasionally, you will get very different measurements! Therefore, you should run the profilers several times and discard outputs that seem like outliers. When it comes to the measurements, do not get fixated on the absolute values (as they change a lot). Instead, observe the relative performance measures as you tweak your implementation. It would be best to use the profilers to gain insight into the performance tradeoff of decisions you make when implementing Graph ADT and Dijkstra's algorithm.
We ask you to run the Driver program, as well as the SystemRuntimeTest and MemoryMonitorTest and report their outcome in your README file, for the following endpoints (using the baltimore.streets.txt file):
JHU to Druid Lake
Starting location: -76.6175,39.3296
Ending location: -76.6383,39.3206
7-11 to Druid Lake
Starting location: -76.6214,39.3212
Ending location: -76.6383,39.3206
Inner Harbor to JHU
Starting location: -76.6107,39.2866
Ending location: -76.6175,39.3296
Please highlight (note in README) if you make an interesting observation, for example, if your program fails to find a path, if the performance changes for different endpoints, etc.
We also provided JmhRuntimeTest, which runs your implementation for the Graph ADT and Dijkstra's algorithm (through Config.java) for the endpoints above. The experiment narrows down to finding the shortest path so you can further hone on optimizing its performance.
The parameters for experimenting (e.g., number of iterations, warm-up, forks, etc.) are chosen to reflect better how JMH profiling is done in practice. With this setting, the JMH profiler will take much longer to experiment. It will report its measurements, including margins of error. Therefore, we encourage you to run JmhRuntimeTest (make sure to run its main method) and report and incorporate its output in your discussion. That said, you are not required to report the output of JmhRuntimeTest in your README file.
Submission
In preparation, you must (1) run checkstyle to ensure your code is checkstyle compliant (if not, fix the styling issues). (2) Create a zip file containing the src folder (and all therein). (3) Submit the zip file to Gradescope.
You can submit as many times as you like until deadline. We will only grade the last submission.
Rubric
Teaching assistants will evaluate your submission using the following criteria:
Please note, we reserve the right to change this rubric without advance notice, even after the submission deadline. However, the chances of doing so are slim, and at any rate, should not be a significant change.
-
Spec 1: There
GraphTest.javacontains a comprehensive suit of tests for unit testing the operations of Graph ADT. [5 points] -
Spec 2: The SparseGraph implementation for inserting a vertex is correct and efficient. [2 point]
-
Spec 3: The SparseGraph implementation for inserting an edge is correct and efficient. [2 point]
-
Spec 4: The SparseGraph implementation for getting the endpoints of an edge are correct and efficient. [2 point]
-
Spec 5: The SparseGraph implementation for removing a vertex is correct and efficient. [2 point]
-
Spec 6: The SparseGraph implementation for removing an edge is correct and efficient. [2 point]
-
Spec 7: The SparseGraph implementation for iterating over vertices and edges (including outgoing and incoming edges for a given vertex) are correct and efficient. [2 point]
-
Spec 8: The SparseGraph implementation for labeling vertices and edges and clearing the labels are correct and efficient. [1 point]
-
Spec 9: The implementation of
DijkstraStreetSearcher.findShortestPathis correct and efficient. [10 points] -
Spec 10: The
README.mdincludes a report of the profiler for exploring Baltimore streets! The report must contain sample runs for "JHU to Druid Lake," "7-11 to Druid Lake," and "Inner Harbor to JHU". [2 point] -
Spec 11: The
README.mdincludes discussion on profiling and benchmarking. [1 point] -
Spec 12: The submission exhibits good practices for writing readable code (such as consistent indentation, etc.) and good programming style (e.g., helper methods are made private, etc.). The code adheres to the formatting standards. [2 point]
The total score for this homework is 33 points.